
Es probable que hayas oído en foros sobre análisis técnico alguna discusión sobre si son mejores los gráficos con los ejes en escala aritmética o logarítmica. En bolsa hay muchos temas en los que no hay evidencia clara sobre qué postura es mejor y por ello lo óptimo es que cada cual utilice lo que le funcione mejor. Bien, este no es el caso aquí y voy a posicionarme fuertemente desde el principio a favor de la escala semi-logarítmica (A veces se usa la palabra logarítmica en vez de semi-logarítmica. Como quedará claro con la explicación posterior lo correcto es aplicar el logaritmo al precio únicamente, el tiempo se mantiene en escala lineal, por eso lo correcto es hablar de escalas semi-logarítmicas o logarítmicas, pero siempre que se aclare que el logaritmo se aplica solo al precio.) En el resto del artículo intentaré exponer de forma clara y sencilla la explicación que sostiene esta postura.
En primer lugar, hay argumentos que parten exclusivamente del propio chartismo y que ya serían suficientes por sí mismos para justificar el uso de la escala semi-logarítmica. Esta parte se la dejo a Carlos Doblado, que en este artículo explica esta materia de forma magistral con su estilo característico.
Yo me voy a centrar en un enfoque algo más técnico, pero también menos trillado. Voy a justificar la escala semi-logarítmica desde el punto de vista económico y financiero.
Para ello es necesario partir de la famosa fórmula del interés compuesto: C0·(1+i)n·t donde C0 es el capital con el que se parte, i es el tipo de interés a aplicar, t es el número de veces que se capitaliza en un año y n es el número de años que se va a capitalizar. Para quien esté menos familiarizado con las matemáticas financieras, capitalizar significa que el interés se añade al capital y a partir de ahí también genera intereses. Por poner un ejemplo rápido, si tenemos 1.000 a los que aplicar un 1% anual de interés capitalizado año a año, al finalizar el primer año tendremos 1.000€ más 10€ de intereses. El segundo año el 1% de interés sin embargo ya no se aplicará sobre los 1.000€, sino sobre los 1.010€, y así sucesivamente.
Lo interesante de esto es que, si el periodo de capitalización se hace más breve, t aumenta, ya que en un año se capitaliza más veces. Supongamos que se acorta este plazo hasta que se capitaliza cada segundo, cada milésima de segundo… así t tiende a infinito y convenientemente la fórmula del interés compuesto pasa a convertirse, con las convenientes transformaciones, en esta: C0·en·t . Esta fórmula es la del interés continuo y se usa cuando sobre una cantidad se capitalizan los intereses de forma continua, de tal forma que nada más devengarse el interés ya se capitaliza inmediatamente.
Esta puede parecer una más de esas simplificaciones que hacen los economistas para poder trabajar con expresiones matemáticas más sencillas. Sin embargo, sí hay un lugar en el que a una cantidad de dinero se le aplica un porcentaje de incremento o decremento cada día, cada hora y cada segundo; los mercados financieros. Cuando una acción es muy volátil y oscila alrededor de un valor medio tanto hacia arriba como hacia abajo sin que haya una tendencia clara, estos efectos de capitalización se anulan, ya que el movimiento a lo largo del periodo no es lo suficientemente grande en términos porcentuales.
Sin embargo, cuando una acción adopta en un periodo determinado una tendencia marcada, aparece un efecto exponencial que hace que la pendiente de la tendencia aumente cada vez más. Esto tiene sentido, ya que en bolsa las cantidades fijas tienen poco significado; los inversores se mueven en términos de porcentajes, y por tanto lo mismo hace el mercado. Imaginemos una acción que está en tendencia alcista y solo sube. Si cada día incrementara el precio en una misma cantidad fija, llegaría un momento en que los incrementos serían absurdos en proporción a la cotización. Lo normal sería que la acción subiera en un porcentaje fijo, en cuyo caso el gráfico de precios en función del tiempo se parecerá mucho a la función exponencial del interés continuo.
Poniendo números esto se ve muy claramente. Si cogemos el Dow Jones Industrial Average (DJIA) vemos que es normal que en un día la cotización se mueva 100 o 200 puntos. Sin embargo, cuando el índice cotizaba en el entorno de los 1.000 puntos a finales de la década de los ‘70 este movimiento hubiera sido totalmente desproporcionado. En el gráfico que puedes ver a continuación se ve perfectamente este efecto de crecimiento geométrico.

Sin embargo, en el siguiente gráfico que muestra el mismo índice en una escala semi-logarítmica puedes ver que la razón de crecimiento ha sido siempre la misma y cercana al 0’04% diario o el 10% anual para el periodo que va hasta 1999.

No obstante, este efecto de crecimiento geométrico en vez de aritmético supone un problema muy claro cuando para realizar un análisis técnico se usa un gráfico en escala aritmética, ya que para el chartismo es vital la medición de distancias y tamaños de patrones. Además, cuando se analiza una tendencia es imprescindible analizar si se producen incrementos en su aceleración o si estos se deben a la apariencia creada por la escala aritmética. Aquí es donde entra en juego el hecho de aplicar la escala semi-logarítmica, que no es otra cosa que aplicar la función logaritmo neperiano al precio para eliminar el efecto potencial y convertir el crecimiento en lineal. Esta última parte es más técnica, pero basta con quedarse con la idea de que haciendo eso se convierte el crecimiento del precio de una curva exponencial a una recta.
Hay que tener en cuenta que la mente humana funciona bien con predicciones lineales, pero las funciones no lineales se escapan a nuestra capacidad de proyección. Es fácil obtener una constatación de esto. Si el lector cogiera un tirachinas y disparara contra una botella es relativamente fácil, a una distancia razonable, que acierte. Sin embargo, con un mecanismo estilo catapulta la probabilidad de acertar disminuye, no digamos ya con artefactos que generen otras trayectorias más exóticas. Esto demuestra la buena capacidad de predicción lineal de nuestro cerebro frente a la peor predicción parabólica en este caso.
En los dos gráficos de abajo se ilustra este efecto. En el primero tenemos el DJIA en escala aritmética haciendo un patrón de doble suelo. Si proyectamos la distancia desde los suelos hasta el máximo intermedio hacia arriba desde el máximo como dice la teoría obtenemos un objetivo en los 10.500 puntos.
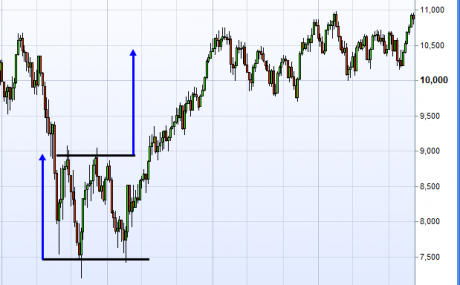
Sin embargo, si hacemos lo mismo en el gráfico de la derecha en escala semi-logarítmica vemos que el objetivo es notablemente más alto y que el precio llegó hasta él, por lo que usando la escala aritmética nos hubiéramos perdido gran parte de la subida. Tendríamos que haber compensado mentalmente el efecto de la deformación exponencial del gráfico, cosa casi imposible.

Por todos estos motivos, la escala semi-logarítmica debe usarse con preferencia a la aritmética, ya que esta primera permite ver los movimientos en términos de porcentajes y rentabilidad que es como deberían verse. Si nuestra capacidad analítica tiene puntos ciegos, lo único que puede hacer un inversor inteligente es utilizar las herramientas que adapten la realidad a aquellos entornos en los que su mente funciona mejor.
